The goal of affinitymatrix is to provide a set of tools to estimate matching models without frictions and with Transferable Utility starting from matched data. The package contains a set of functions to implement the tools developed by Dupuy and Galichon (2014), Dupuy, Galichon and Sun (2019) and Ciscato, Galichon and Gousse (2020).
estimate.affinity.matrix estimates the affinity matrix of the matching model of Dupuy and Galichon (2014), performs the saliency analysis and the rank tests. The user must supply a matched sample that is treated as the equilibrium matching of a bipartite one-to-one matching model without frictions and with Transferable Utility. For the sake of clarity, in the documentation we take the example of the marriage market and refer to “men” as the observations on one side of the market and to “women” as the observations on the other side. Other applications may include matching between CEOs and firms, firms and workers, buyers and sellers, etc. An example is provided below.
estimate.affinity.matrix.lowrank estimates the affinity matrix of the matching model of Dupuy and Galichon (2014) under a rank restriction on the affinity matrix, as suggested by Dupuy, Galichon and Sun (2019). In their own words, “to accommodate high dimensionality of the data, they propose a novel method that incorporates a nuclear norm regularization which effectively enforces a rank constraint on the affinity matrix.” This function also performs the saliency analysis and the rank tests. This function is a potential alternative to estimate.affinity.matrix when the number of matching variables is low relatively to the number of observed matches or when the researcher believes that the number of dimensions of the matching problem is much lower than the number of observed variables considered.
estimate.affinity.matrix.unipartite estimates the affinity matrix of the matching model of Ciscato, Gousse and Galichon (2020), performs the saliency analysis and the rank tests. The model is called unipartite (otherwise known as the “roommate problem”) and differs from the original Dupuy and Galichon (2014) since all agents are pooled in one group and can match within the group. For the sake of clarity, in the documentation we take the example of the same-sex marriage market and refer to “first partner” and “second partner” in order to distinguish between the arbitrary partner order in a database (e.g., survey respondent and partner of the respondent). Note that in this case the variable “sex” is treated as a matching variable rather than a criterion to assign partners to one side of the market as in the bipartite case. Other applications may include matching between coworkers, roommates or teammates.
You can install the released version of affinitymatrix directly from Github with:
The example below shows how to use the main function of the package, estimate.affinity.matrix, and how to summarize its findings. We first generate a random sample of matches: the values of the normalized variance-covariance matrix used in the data generating process are taken from Chiappori, Ciscato and Guerriero (2020). For the sake of clarity, consider the marriage market example: every row of our data frame corresponds to a couple. The first Kx columns correspond to the husbands’ characteristics, or matching variables, while the last Ky columns correspond to the wives’. The key inputs to feed to estimate.affinity.matrix are two matrices X and Y corresponding to the husbands’ and wives’ traits and sorted so that the i-th man in X is married to the i-th woman in Y.
# Load
library(affinitymatrix)
# Parameters
Kx = 4; Ky = 4; # number of matching variables on both sides of the market
N = 100 # sample size
mu = rep(0, Kx+Ky) # means of the data generating process
Sigma = matrix(c(1, 0.326, 0.1446, -0.0668, 0.5712, 0.4277, 0.1847, -0.2883, 0.326, 1, -0.0372, 0.0215, 0.2795, 0.8471, 0.1211, -0.0902, 0.1446, -0.0372, 1, -0.0244, 0.2186, 0.0636, 0.1489, -0.1301, -0.0668, 0.0215, -0.0244, 1, 0.0192, 0.0452, -0.0553, 0.2717, 0.5712, 0.2795, 0.2186, 0.0192, 1, 0.3309, 0.1324, -0.1896, 0.4277, 0.8471, 0.0636, 0.0452, 0.3309, 1, 0.0915, -0.1299, 0.1847, 0.1211, 0.1489, -0.0553, 0.1324, 0.0915, 1, -0.1959, -0.2883, -0.0902, -0.1301, 0.2717, -0.1896, -0.1299, -0.1959, 1),
nrow=Kx+Ky) # (normalized) variance-covariance matrix of the data generating process
labels_x = c("Educ.", "Age", "Height", "BMI") # labels for men's matching variables
labels_y = c("Educ.", "Age", "Height", "BMI") # labels for women's matching variables
# Sample
data = MASS::mvrnorm(N, mu, Sigma) # generating sample
X = data[,1:Kx]; Y = data[,Kx+1:Ky] # men's and women's sample data
w = sort(runif(N-1)); w = c(w,1) - c(0,w) # sample weights
# Main estimation
res = estimate.affinity.matrix(X, Y, w = w, nB = 500)
#> Setup...
#> Main estimation...
#> Saliency analysis...
#> Rank tests...
#> Saliency analysis (bootstrap)...The output of estimate.affinity.matrix is a list of objects that constitute the estimation results. The estimated affinity matrix is stored under Aopt, while the vector of loadings describing men’s and women’s matching factors are stored under U and V respectively. The following functions can be used to produce summaries of the different findings. For further details, Chiappori, Ciscato and Guerriero (2020) contain tables and plots that are generated with these functions.
# Print affinity matrix with standard errors
table1 = show.affinity.matrix(res, labels_x = labels_x, labels_y = labels_y)
# Here we print a Markdown version: we recommend using the function export.table to store the tables in a txt file
# export.table(table1, name = "affinity_matrix", "path = "myresults")
gsub("\\}", "***", gsub("\\\\|hline|textbf\\{|\t|&|\n", "", table1))
#> [,1] [,2] [,3] [,4] [,5]
#> [1,] "" "Educ." "Age" "Height" "BMI"
#> [2,] "Educ." "1.12***" "0.39" "0.08" "-0.45***"
#> [3,] "" "(0.25) " "(0.34) " "(0.18) " "(0.18) "
#> [4,] "Age" "-0.52" "4.48***" "0.98***" "0.69***"
#> [5,] "" "(0.35) " "(0.71) " "(0.29) " "(0.28) "
#> [6,] "Height" "0.15" "0.41" "0.10" "-0.12"
#> [7,] "" "(0.17) " "(0.26) " "(0.13) " "(0.13) "
#> [8,] "BMI" "0.78***" "0.14" "0.10" "0.07"
#> [9,] "" "(0.19) " "(0.27) " "(0.14) " "(0.14) "
# Print diagonal elements of the affinity matrix with standard errors
table2 = show.diagonal(res, labels = labels_x)
# export.table(table2, name = "diagonal_affinity_matrix", "path = "myresults")
gsub("\\}", "***", gsub("\\\\|hline|textbf\\{|\t|&|\n", "", table2))
#> [,1] [,2] [,3] [,4]
#> [1,] "Educ." "Age" "Height" "BMI"
#> [2,] "1.12***" "4.48***" "0.10" "0.07"
#> [3,] "(0.25)" "(0.71)" "(0.13)" "(0.14)"
# Print rank test summary
table3 = show.test(res)
# export.table(table3, name = "rank_tests", "path = "myresults")
gsub("\\}", "***", gsub("\\\\|hline|textbf\\{|\t|&|\n", "", table3))
#> [,1] [,2] [,3] [,4]
#> [1,] "$H_0$: $rk(A)=k$" "$k=1$" "$k=2$" "$k=3$"
#> [2,] "$chi^2$" "36.55" "6.62" "0.06"
#> [3,] "$df$" "9" "4" "1"
#> [4,] "Rejected?" "Yes" "No" "No"
# Print results from saliency analysis
table4 = show.saliency(res, labels_x = labels_x, labels_y = labels_y, ncol_x = 2, ncol_y = 2)
# export.table(table4$U.table, name = "saliency_men", "path = "myresults")
# export.table(table4$V.table, name = "saliency_women", "path = "myresults")
gsub("\\}", "***", gsub("\\\\|hline|textbf\\{|\t|&|\n|$", "", table4$U.table))
#> [,1] [,2] [,3]
#> [1,] "" "Index 1" "Index 2"
#> [2,] "Educ." "0.05" "0.85***"
#> [3,] "Age" "1.00***" "-0.06***"
#> [4,] "Height" "0.08" "0.16"
#> [5,] "BMI" "0.02" "0.51***"
#> [6,] " Index share" "0.72" "0.22"
gsub("\\}", "***", gsub("\\\\|hline|textbf\\{|\t|&|\n|$", "", table4$V.table))
#> [,1] [,2] [,3]
#> [1,] "" "Index 1" "Index 2"
#> [2,] "Educ." "-0.09***" "0.95***"
#> [3,] "Age" "0.96***" "0.12***"
#> [4,] "Height" "0.21***" "0.05"
#> [5,] "BMI" "0.14***" "-0.28***"
#> [6,] " Index share" "0.72" "0.22"
# Show correlation between observed variables and matching factors
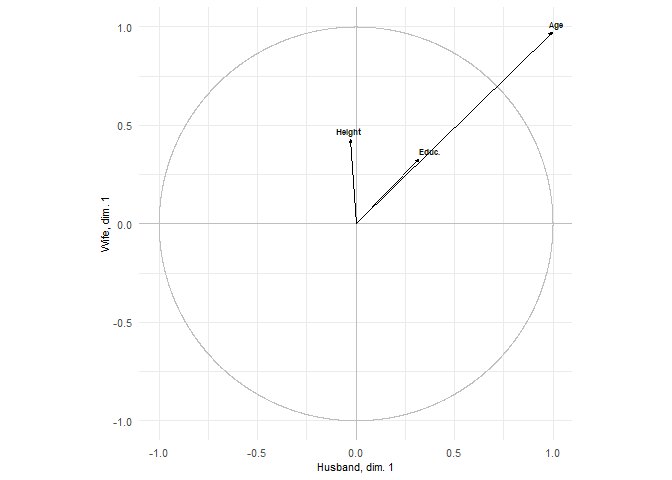
plots = show.correlations(res, labels_x = labels_x, labels_y = labels_y,
label_x_axis = "Husband", label_y_axis = "Wife")
# for (d in 1:length(plots)) ggsave(paste0("myresults/plot_",d) plot = plots[d])
plots[1]
#> [[1]]

Ciscato, Edoardo, Alfred Galichon, and Marion Gousse. “Like attract like? a structural comparison of homogamy across same-sex and different-sex households.” Journal of Political Economy 128, no. 2 (2020): 740-781.
Chiappori, Pierre-André, Edoardo Ciscato, and Carla Guerriero. “Analyzing matching patterns in marriage: theory and application to Italian data.” HCEO Working Paper no. 2020-080 (2020).
Dupuy, Arnaud, and Alfred Galichon. “Personality traits and the marriage market.” Journal of Political Economy 122, no. 6 (2014): 1271-1319.
Dupuy, Arnaud, Alfred Galichon, and Yifei Sun. “Estimating matching affinity matrices under low-rank constraints.” Information and Inference: A Journal of the IMA 8, no. 4 (2019): 677-689.