paleopop is an extension to poems, a spatially-explicit, process-explicit, pattern-oriented framework for modeling population dynamics. This extension adds functionality for modeling large populations at generational time-steps over paleontological time-scales.
You can install the development version from GitHub with:
poems and paleopop are based on R6 class objects. R is primarily a functional programming language; if you want to simulate a population, you might use the lapply or replicate functions to repeat a generative function like rnorm. R6 creates an object-oriented programming language inside of R, so instead of using functions on other functions, in these packages we simulate populations using methods attached to objects. Think of R6 objects like machines, and methods like switches you can flip on the machines.
One of the major additions in paleopop is the PaleoRegion R6 class, which allows for regions that change over time due to ice sheets, sea level, bathymetry, and so on. The plots below show the temporal mask functionality of the PaleoRegion object. The temporal mask indicates cells that are occupiable at each time step with a 1 and unoccupiable cells with a NA. In this example, I use the temporal_mask_raster method to show how “Ring Island” changes at time step 10 due to a drop in sea level.
library(poems)
library(paleopop)
coordinates <- data.frame(x = rep(seq(-178.02, -178.06, -0.01), 5),
y = rep(seq(19.02, 19.06, 0.01), each = 5),
z = rep(1, 25))
template_raster <- raster::rasterFromXYZ(coordinates,
crs = "+proj=longlat +datum=WGS84 +ellps=WGS84 +towgs84=0,0,0")
sealevel_raster <- template_raster
template_raster[][c(7:9, 12:14, 17:19)] <- NA # make Ring Island
sealevel_raster[][c(7:9, 12:14, 17:18)] <- NA
raster_stack <- raster::stack(x = append(replicate(9, template_raster), sealevel_raster))
region <- PaleoRegion$new(template_raster = raster_stack)
raster::plot(region$temporal_mask_raster()[[1]], main = "Ring Island (first timestep)",
xlab = "Longitude (degrees)", ylab = "Latitude (degrees)",
colNA = "blue")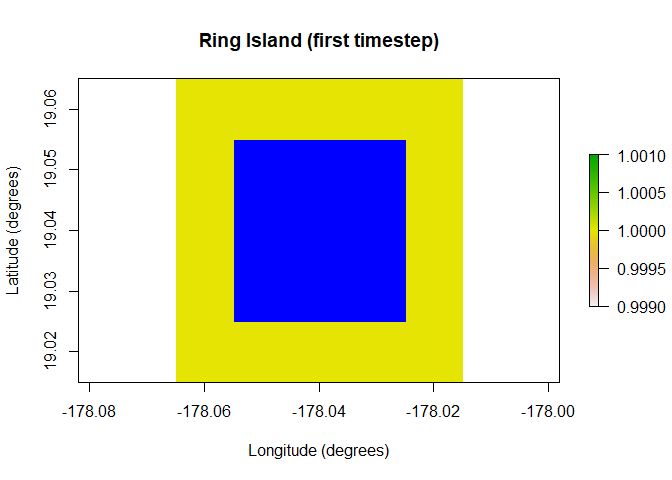
raster::plot(region$temporal_mask_raster()[[10]], main = "Ring Island (last timestep)",
xlab = "Longitude (degrees)", ylab = "Latitude (degrees)",
colNA = "blue")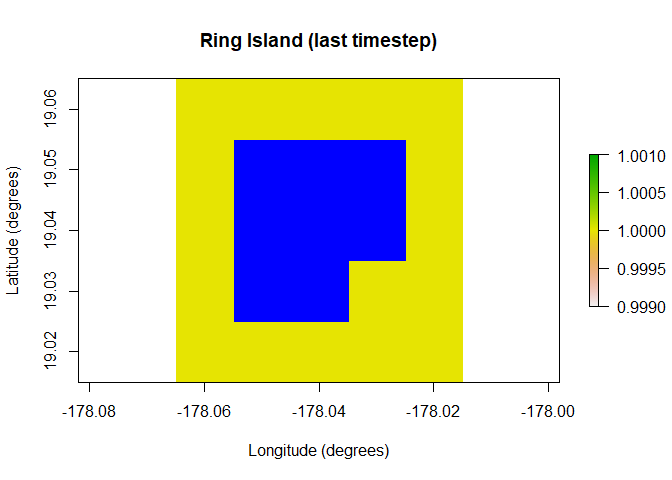
paleopop also includes the PaleoPopModel class, which sets up the population model structure. Here I show a very minimalist setup of a model template using this class.
model_template <- PaleoPopModel$new(
region = region, # makes the simulation spatially explicit
time_steps = 10, # number of time steps to simulate
years_per_step = 12, # years per generational time-step
standard_deviation = 0.1, # SD of growth rate
growth_rate_max = 0.6, # maximum growth rate
harvest = F, # are the populations harvested?
populations = 17, # total occupiable cells over time
initial_abundance = seq(9000, 0, -1000), # initial pop. sizes
transition_rate = 1.0, # transition rate between generations
carrying_capacity = rep(1000, 17), # static carrying capacity
dispersal = (!diag(nrow = 17, ncol = 17))*0.05, # dispersal rates
density_dependence = "logistic", # type of density dependence
dispersal_target_k = 10, # minimum carrying capacity to attract dispersers
occupancy_threshold = 1, # lower than this # of pops. means extinction
abundance_threshold = 10, # threshold for Allee effect
results_selection = c("abundance") # what outputs do you want in results?
)The paleopop_simulator function accepts a PaleoPopModel object or a named list as input to simulate populations over paleo time scales, and the PaleoPopResults class stores the outputs from the paleo population simulator.
results <- paleopop_simulator(model_template)
results # examine
#> $abundance
#> [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
#> [1,] 39 74 150 252 424 666 667 766 871 995
#> [2,] 117 229 374 528 670 930 777 878 832 963
#> [3,] 1345 1063 913 938 1006 846 764 967 801 765
#> [4,] 27 63 99 171 315 531 825 905 1081 898
#> [5,] 382 532 707 846 979 940 1065 931 1023 977
#> [6,] 523 715 876 1062 1113 1092 1355 1377 922 684
#> [7,] 739 906 872 916 1183 1164 1086 1047 918 972
#> [8,] 1238 1230 1400 1011 1093 1209 1184 1208 1007 953
#> [9,] 1178 1100 954 999 916 831 745 881 928 1049
#> [10,] 0 0 0 0 0 0 0 0 0 0
#> [11,] 0 0 0 0 0 0 0 0 0 0
#> [12,] 0 0 0 0 0 0 0 0 0 0
#> [13,] 450 615 682 811 852 1035 984 951 1042 1055
#> [14,] 174 258 377 603 779 889 934 978 974 942
#> [15,] 600 805 948 919 887 926 1043 867 1003 866
#> [16,] 1313 882 1015 1052 1020 964 925 1003 1008 1049
#> [17,] 904 1035 983 1154 1043 887 907 1043 969 940
raster::plot(region$raster_from_values(results$abundance[,10]),
main = "Final abundance", xlab = "Longitude (degrees)",
ylab = "Latitude (degrees)", colNA = "blue")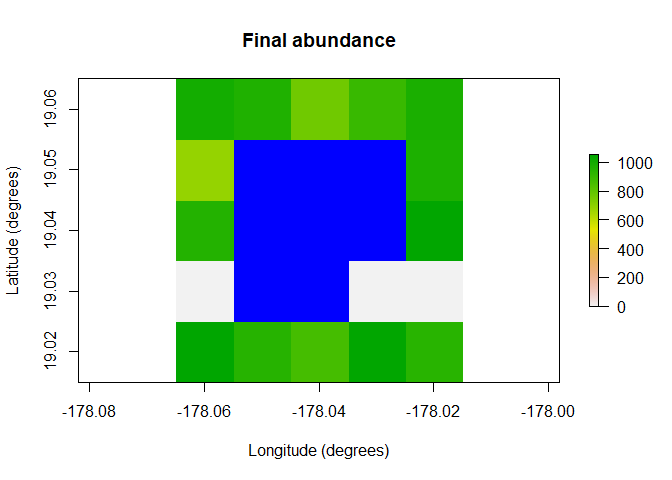
A practical example of how to use paleopop, with more complex parameterization, can be found in the vignette.