

skpr is an open source design of experiments suite for generating and evaluating optimal designs in R. Here is a sampling of what skpr offers:
# To install:
install.packages("skpr")
# To install the latest version from Github:
# install.packages("devtools")
devtools::install_github("tylermorganwall/skpr")gen_design() generates optimal designs from a candidate
set, given a model and the desired number of runs.eval_design() evaluates power parametrically for linear
models, for normal and split-plot designs.eval_design_mc() evaluates power with a Monte Carlo
simulation, for linear and generalized linear models. This function also
supports calculating power for split-plot designs using REML.eval_design_survival_mc() evaluates power with a Monte
Carlo simulation, allowing the user to specify a point at which the data
is censored.eval_design_custom_mc() allows the user to import their
own libraries and use the Monte Carlo framework provided by skpr to
calculate power.skprGUI() and skprGUIbrowser() opens up
the GUI in either R Studio or an external browser.If addition, the package offers two functions to generate common plots related to designs:
plot_correlations() generates a color map of
correlations between variables.plot_fds() generates the fraction of design space plot
for a given design.##skprGUI
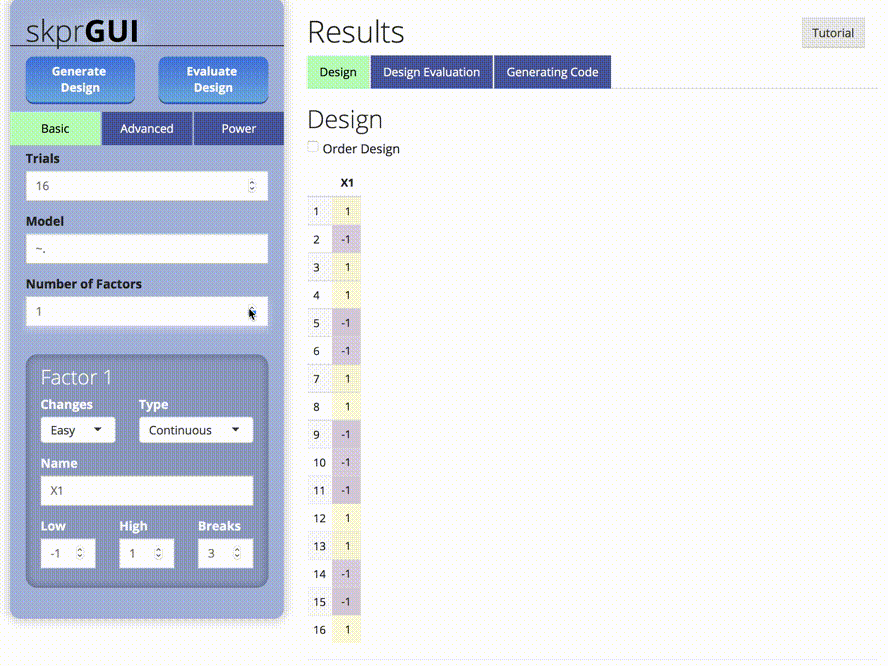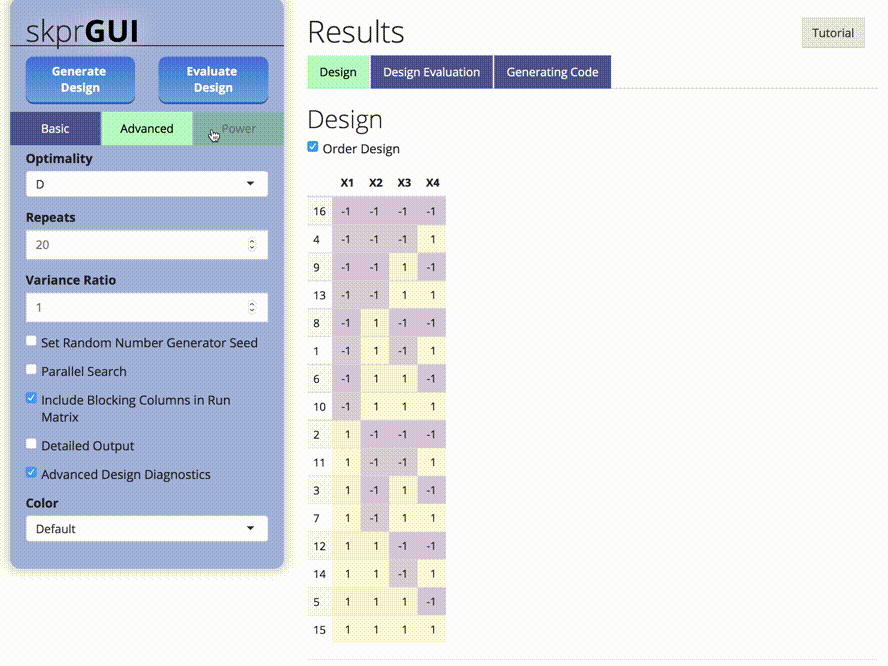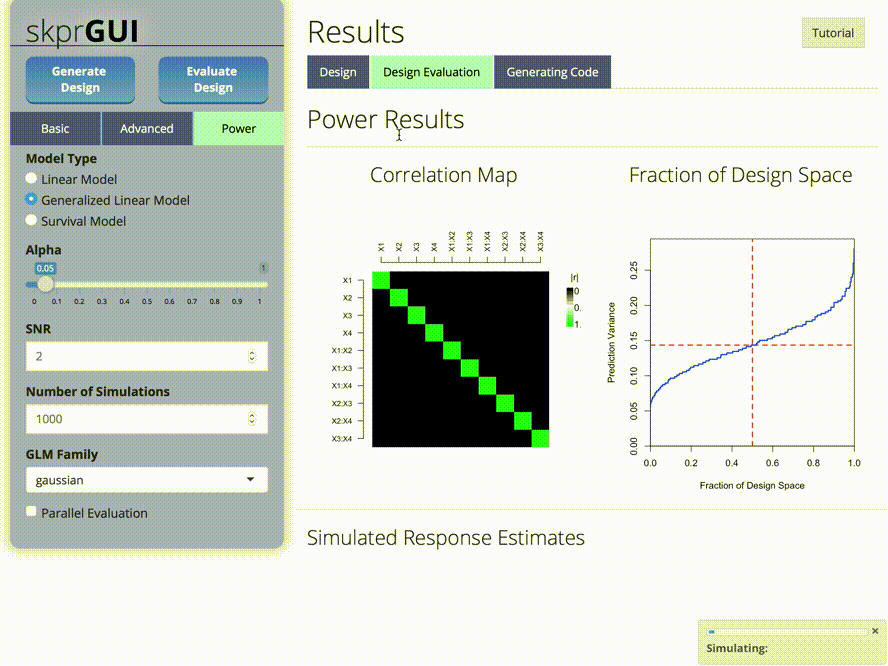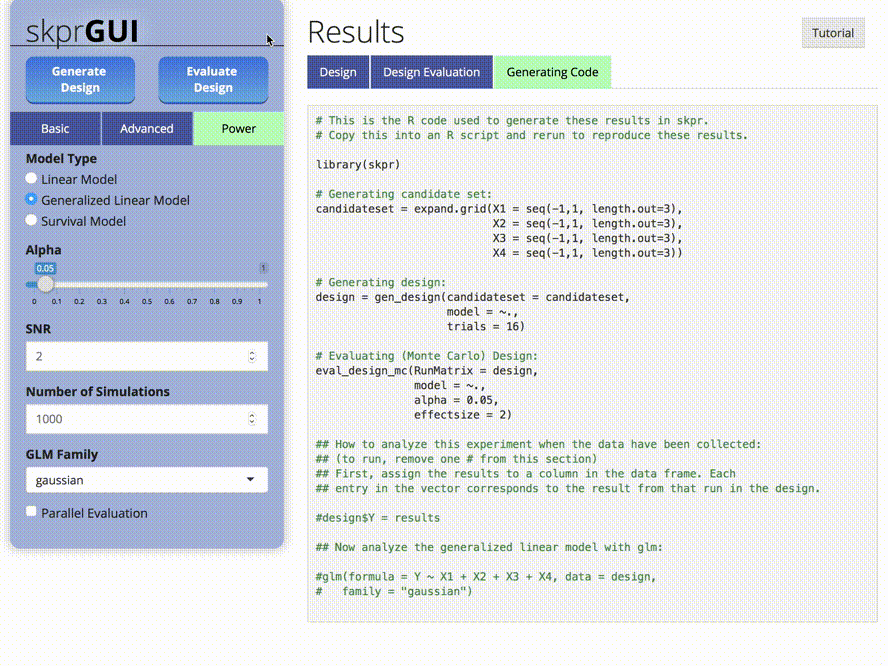
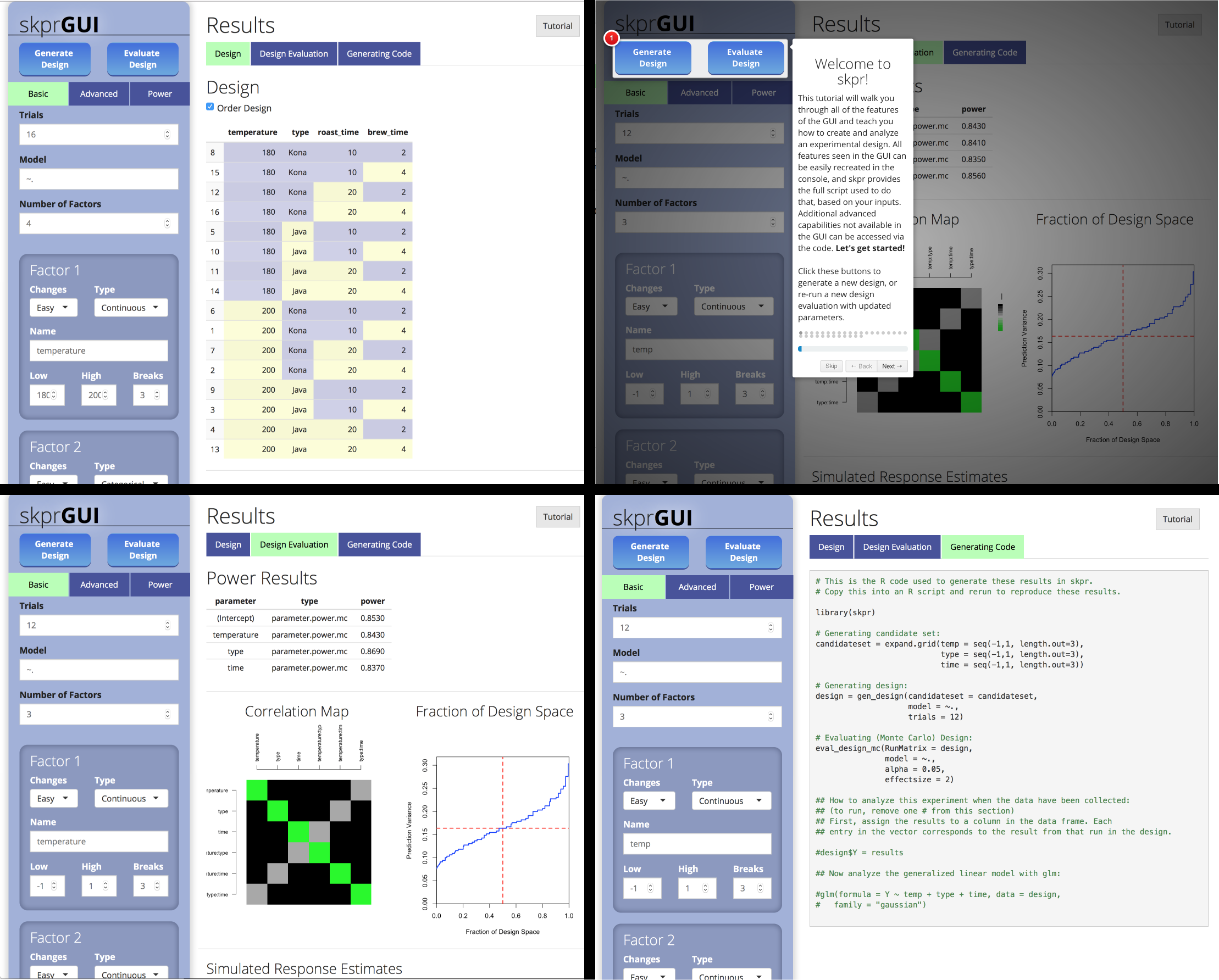
skprGUI provides an graphical user interface to access all of the
main features of skpr. An interactive tutorial is provided to
familiarize the user with the available functionality. Type
skprGUI() or skprGUIbrowser() to begin.
Screenshots:
library(skpr)
#Generate a candidate set of all potential design points to be considered in the experiment
#The hypothetical experiment is determining what affects the caffeine content in coffee
candidate_set = expand.grid(temp = c(80,90,100),
type = c("Kona","Java"),
beansize = c("Large","Medium","Small"))
candidate_set
#> temp type beansize
#> 1 80 Kona Large
#> 2 90 Kona Large
#> 3 100 Kona Large
#> 4 80 Java Large
#> 5 90 Java Large
#> 6 100 Java Large
#> 7 80 Kona Medium
#> 8 90 Kona Medium
#> 9 100 Kona Medium
#> 10 80 Java Medium
#> 11 90 Java Medium
#> 12 100 Java Medium
#> 13 80 Kona Small
#> 14 90 Kona Small
#> 15 100 Kona Small
#> 16 80 Java Small
#> 17 90 Java Small
#> 18 100 Java Small
#Generate the design (default D-optimal)
design = gen_design(candidateset = candidate_set,
model = ~temp + type + beansize,
trials=12)
design
#> temp type beansize
#> 1 80 Java Medium
#> 2 100 Java Large
#> 3 100 Java Small
#> 4 80 Java Large
#> 5 80 Kona Medium
#> 6 80 Kona Small
#> 7 100 Kona Small
#> 8 100 Kona Medium
#> 9 80 Kona Large
#> 10 100 Java Medium
#> 11 100 Kona Large
#> 12 80 Java Small
#Evaluate power for the design with an allowable type-I error of 5% (default)
eval_design(design)
#> parameter type power
#> 1 (Intercept) effect.power 0.8424665
#> 2 temp effect.power 0.8424665
#> 3 type effect.power 0.8424665
#> 4 beansize effect.power 0.5165386
#> 5 (Intercept) parameter.power 0.8424665
#> 6 temp parameter.power 0.8424665
#> 7 type1 parameter.power 0.8424665
#> 8 beansize1 parameter.power 0.5593966
#> 9 beansize2 parameter.power 0.5593966
#> ============Evaluation Info============
#> • Alpha = 0.05 • Trials = 12 • Blocked = FALSE
#> • Evaluating Model = ~temp + type + beansize
#> • Anticipated Coefficients = c(1.000, 1.000, 1.000, 1.000, -1.000)
#Evaluate power for the design using a Monte Carlo simulation.
#Here, we set the effect size (here, the signal-to-noise ratio) to 1.5.
eval_design_mc(design, effectsize=1.5)
#> parameter type power
#> 1 (Intercept) effect.power.mc 0.600
#> 2 temp effect.power.mc 0.612
#> 3 type effect.power.mc 0.610
#> 4 beansize effect.power.mc 0.316
#> 5 (Intercept) parameter.power.mc 0.600
#> 6 temp parameter.power.mc 0.612
#> 7 type1 parameter.power.mc 0.610
#> 8 beansize1 parameter.power.mc 0.359
#> 9 beansize2 parameter.power.mc 0.354
#> ===========Evaluation Info============
#> • Alpha = 0.05 • Trials = 12 • Blocked = FALSE
#> • Evaluating Model = ~temp + type + beansize
#> • Anticipated Coefficients = c(0.750, 0.750, 0.750, 0.750, -0.750)
#Evaluate power for the design using a Monte Carlo simulation, for a non-normal response.
#Here, we also increase the number of simululations to improve the precision of the results.
eval_design_mc(design, nsim=5000, glmfamily = "poisson", effectsize=c(2,6))
#> parameter type power
#> 1 (Intercept) effect.power.mc 0.9968
#> 2 temp effect.power.mc 0.9826
#> 3 type effect.power.mc 0.9832
#> 4 beansize effect.power.mc 0.8502
#> 5 (Intercept) parameter.power.mc 0.9968
#> 6 temp parameter.power.mc 0.9826
#> 7 type1 parameter.power.mc 0.9832
#> 8 beansize1 parameter.power.mc 0.8842
#> 9 beansize2 parameter.power.mc 0.7052
#> ============Evaluation Info============
#> • Alpha = 0.05 • Trials = 12 • Blocked = FALSE
#> • Evaluating Model = ~temp + type + beansize
#> • Anticipated Coefficients = c(1.242, 0.549, 0.549, 0.549, -0.549)
#skpr was designed to operate with the pipe (%>%) in mind.
#Here is an example of an entire design of experiments analysis in three lines:
expand.grid(temp = c(80,90,100), type = c("Kona","Java"), beansize = c("Large","Medium","Small")) %>%
gen_design(model = ~temp + type + beansize + beansize:type + I(temp^2), trials=24, optimality="I") %>%
eval_design_mc()
#> parameter type power
#> 1 (Intercept) effect.power.mc 0.912
#> 2 temp effect.power.mc 0.927
#> 3 type effect.power.mc 0.997
#> 4 beansize effect.power.mc 0.935
#> 5 I(temp^2) effect.power.mc 0.637
#> 6 type:beansize effect.power.mc 0.913
#> 7 (Intercept) parameter.power.mc 0.912
#> 8 temp parameter.power.mc 0.927
#> 9 type1 parameter.power.mc 0.997
#> 10 beansize1 parameter.power.mc 0.917
#> 11 beansize2 parameter.power.mc 0.913
#> 12 I(temp^2) parameter.power.mc 0.637
#> 13 type1:beansize1 parameter.power.mc 0.899
#> 14 type1:beansize2 parameter.power.mc 0.902
#> ==============Evaluation Info==============
#> • Alpha = 0.05 • Trials = 24 • Blocked = FALSE
#> • Evaluating Model = ~temp + type + beansize + type:beansize + I(temp^2)
#> • Anticipated Coefficients = c(1.000, 1.000, 1.000, 1.000, -1.000, 1.000, 1.000, -1.000)